Must We Randomize Our Experiment?

Report No. 47

George Box
Copyright © 1989, Used by Permission

Practical Significance

The importance of randomization in the running of valid experiments in an industrial context is sometimes questioned. In this report the essential issues are discussed and guidance is provided.

Keywords: Randomization, Non-stable Systems, Nonstationarity, Design of Experiments

*This report will appear as #2 in the series to be called "George's Column" in the Journal of Qualily Engineering (1990).

"My guru says you must always randomize."

"My guru says you don't need to."

"You should never run an experiment unless you are sure the system (the process, the pilot plant, the lab operation) is in a state of control."

"Randomization would make my experiment impossible to run."

"I took a course in statistics and all the theory worked out perfectly without any randomization."

We have all heard statements like these. What are we to conclude?

The Problem of Running Experiments in the Real World

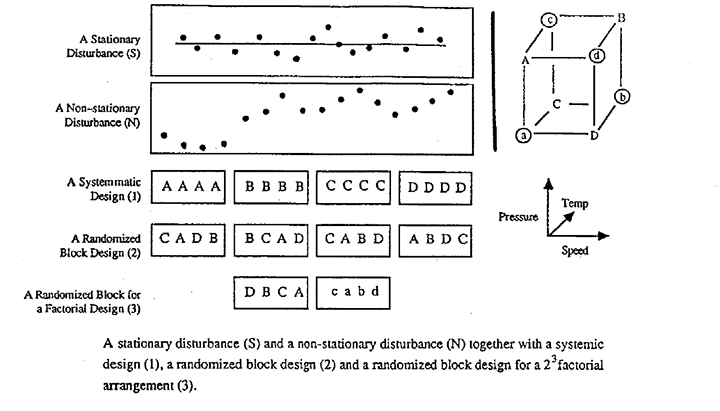
The statistical design of experiments was invented almost seventy years ago by Sir Ronald Fisher. His objective was to make it possible to run informative and unambiguous experiments not just in the laboratory but in the real world outside the laboratory. Initially his experimental material was agricultural land. Not only did this land vary a great deal as you went from one experimental plot to the next, but the yields from successive plots were related to each other. Suppose that if no treatment was applied so that the "disturbance" you saw was merely "error", then the yields from successive plots would not look like the random stationary disturbance (S) in the figure, which is a picture of an ideal process in a state of control with results varying randomly about a fixed mean. Instead they might look like the non-stationary process N where a high yielding plot was likely to be followed by another high yielding plot and visa versa. So the background disturbance against which the effect of different treatments had to be judged varied in a highly non-random - unstable - non-stationary way. Fisher's problem was how to run valid comparative experiments in this situation.

Is Your Experimental System in a State of Statistical Control?

The problem that Fisher considered is not confined to agricultural experimentation. To see if you believe in random stationarity in your particular kind of work, think of the size of chance differences you expect in measurements taken m steps apart (in time or in space). Random variation about a fixed mean implies that the variation in such differences remains the same whether the measurements are taken one step apart or one hundred steps apart. If you believe instead the variation would, on the average, continually increase as the distance apart became greater, then you don't believe in starionarity.*

The truth is that we all live in a non-stationary world; a world in which external factors never stay still. Indeed the idea of stationarity - of a stable world in which, without our intervention, things stay put over time - is a purely conceptual one. The concept of stationarity is useful only as a background against which the real non-stationary world can be judge. For example, the manufacture of parts is an operation involving machines and people. But the parts of a machine are not fixed entities. They are wearing out, changing their dimensions, and losing their adjustment. The behavior of the people who run the machines is not fixed either. A single operator forgets things over time and alters what he does. When a number of operators are involved, the opportunities for change because of failures to communicate are further multiplied. Thus, if left to itself any process will drift away from its initial state. It would be nice if uniformity could be achieved, once and for all, by carefully adjusting a machine, giving appropriate instructions to operators, and letting it run, but unfortunately this would rarely, if ever, result in the production of uniform product. Extraordinary precautions are needed in practice to ensure that the system does not drift away from the target value and that it behaves like the stationary process (S).

So the first thing we must understand is that stationarity, and hence the uniformity of everything depending on it, is an unnatural state that requires a great deal of effort to achieve. That is why good quality control takes so much effort and is so important. All of this is true, not only for manufacturing processes, but for any operation that we would like to be done consistently, such as the taking of blood pressures in a hospital or the performing of chemical analyses in a laboratory. Having found the best way to do it, we would like it to be done that way consistently, but experience shows that very careful planning, checking, recalibration and sometimes appropriate intervention, is needed to ensure that this happens.

*Standard courses in mathematical statistics have not helped, since they often assume a stationary disturbance. Specifically, they usually suppose that the disturbance consists of errors that vary independently about a fixed mean or about a fixed model. Studies of the effects of discrepancies from such a model have usually concerned such questions as what would happen if the data followed a non-normal (but still stationary) process. However, discrepancies due to non-normality are usually trivial compared with those arising from non-stationarity.

Performing Experiments in a Nonstationary Environment

So what did Fisher suggest we do about running experiments in this non-stationary world? For illustration suppose we had four different methods/treatments/procedures (A, B, C, and D) to compare, and we wanted to test each method four times over. Fisher suggested that rather than run a systematic design like Design 1 in Figure 1, in which we first ran all the A's, then all the B's and so on, we should run a "randomized block" arrangement like Design 2. In this latter arrangement within each "block" of four you would run each of the treatments A, B, C, and D in random order. *

* [footnote in printed report] The idea of getting rid of external variation by blocking has other uses. The blocks might refer, not to runs made at different periods of time, but to runs made on different machines, or to runs made with different operators. In each case randomization within the blocks would validate the experiment, the subsequent analysis, and the conclusions.

Now frequently Design 1 would be a lot easier to run than Design 2, so it is reasonable to ask "What does Design 2 do for me that Design 1 doesn't?" Well, if we could be absolutely sure that the process disturbance was like S - that throughout the experiment the process was in a perfect state of control with variation random about a fixed mean, then it would make absolutely no difference which design was used. In this case Designs 1 and 2 would be equally good.

But suppose the process disturbance was non-stationary like that marked N in Figure 1. Then it is easy to see that the systematic Design 1 would give invalid results. For example even if the different treatments really had no effect B, C, and D could look very good compared with A simply because the process disturbance happened to be "up" during the dine when the B, C and D runs were being made. On the other hand, if the experiment were run with the randomized Design 2 it would provide valid comparisons of A, B, C and D. Also, the standard methods of statistical analysis would be approximately valid even though they were based on the usual assumptions, including stationarity; that is, the data could be analyzed as if the process had been in a state of control. Not only this, but differences in block averages, which could account for a lot of the variation, would be totally eliminated and the relevant experimental error would be only that which occurred between plots in the same block.

If the experiment was not simply a comparison of different methods like A, B, C and D, but a factorial design like the one in the right of the figure in which speed, pressure and temperature were being tested, you could still use the same idea. As in Design 3, you could put the factorial runs marked A, B, C, and D in the first block and those labeled a, b, c and d in the second. In both cases you would run in random order within the blocks. It would then again turn out that you could calculate the usual contrasts for all the main effects and all the two-factor interactions free from differences between blocks and that you could carry out a standard analysis as if the process had been in a state of control throughout the experiment, if the details of these ideas are unfamiliar, you can find out more about them in any good book on experimental design.

Randomized experiments of this kind made it possible for the first time to conduct valid comparative experiments in the real world outside the laboratory. Thus beginning in the 1920's, valid experimentation was possible not only in agriculture, but also in medicine, biology, forestry, drug testing, opinion surveys, and so forth. Fisher's ideas were quickly introduced into all these areas.

Comparative Experiments

Why do I keep using the term comparative experiments? Experimentation in a non-stationary environment cannot claim to tell us what is the precise result of using, say, treatment A. This must depend to some extent on the state of the environment at the particular time of the experiment (for example, in the agricultural experiment, it would depend on the fertility of the particular soil on which treatment A was tested). What it can do is to make valid comparisons that are likely to hold up in similar circumstances of experimentation.* This is usually all that is needed.

Beginning in the 1930's and 1940's these ideas of experimental design also began to be used in industrial experiments both in Britain and in the U.S. Other designs were developed in England and America in the 1940's and 1950's such as fractional factorial designs and other orthogonal arrays and also variance component designs and response surface designs to meet new problems. These were used particularly in the chemical industry. In all of this, Fisher's basic ideas of randomization and blocking retained their importance because most of the time one could not be sure that disturbances were even approximately in a state of statistical control.

Until fairly recently in this country experimental design had not been used extensively in the "parts" industries (e. g. automobile manufacture for example). Now, however, because of its use by the Japanese, who borrowed these concepts from the West, some of the ideas of experimental design are being re-imported from Japan. In particular this is true of the so-called "Taguchi methods". These methods pay scant attention to randomization and blocking however. So the question is often raised as to whether or not randomization is still important in the "parts" industries.

* [footnote] Note that the question of what are similar circumstances of experimentation must invariably rest on the technical opinion of the person using the results. It is not a statistical question, as has been pointed out by Deming (1950, 1975) in his discussion of enumerative and analytic studies.

What to Do

To understand what we should do in practice, let's look at the problem a little more closely. We have seen that we live in a non-stationary world in which nothing stays put whether we are talking about the process of manufacturing or the taking of a blood pressure reading. But all models are approximations, so the real question is whether the stationary approximation is good enough for your particular situation. According to my argument, if it is, you don't need to randomize. Such questions are not easy - for while the degree of non-stationary in making parts, a for example, usually is very different from that occurring in an agricultural field, the precision needed in making a part is correspondingly much greater and the differences we may be looking for, much smaller. Also even in the automobile industry not all problems are about making parts.

Many experiments (for example, those arising in the paint shop) are conducted in circumstances much less easy to control.

The crucial factor in the effective use of any statistical method is good judgement. All I can do here is to help you use it, and in particular to make clear what it is you must use your good judgement about.

All right then. You do not need to randomize if you believe your system is, to a sufficiently good approximation, in a state of control and can be relied on to stay in that state while you make experimental changes (that presumably you have never made before). Sufficiently good approximation to a state of control means that over the period of experimentation differences due to the slight degree of non-stationarity existing will be small compared with differences due to the treatments. In making such a judgment bear in mind that belief is not the same as wishful thinking.

My advice then would be:

1. In those cases where randomization only slightly complicates the experiment, always randomize.
2. In those cases where randomization would make the experiment impossible or extremely difficult to do, but you can make an honest judgement about approximate stationarity of the kind outlined above, run the experiment anyway without randomization.
3. if you believe the process is so unstable that without randomization the results would be useless and misleading, and randomization would make the experiment impossible or extremely difficult to do, then do not run the experiment. Work instead on stabilizing the process or on getting the information some other way.
4. A compromise design that sometimes helps to overcome some of these difficulties is the split plot arrangement. Maybe I can talk to you about this in a later column.

References

• Deming, W.E. (1950). Some Theory of Sampling, New York: Wiley.
• Deming, W.E. (1975). On Probability as a Basis for Action, American Statistician, Vol. 29, No. 4, pp. 146-152.