Quality Improvement: An Expanding Domain for the Application of Scientific Method

Home - Statistics for Experimenters - Articles - Hunter Award - Comments - Links - Photos

williamghunter.net > George Box Articles > Quality Improvement: An Expanding Domain for the Application of Scientific Method

Quality Improvement: An Expanding Domain for the Application of Scientific Method

Practical Significance

Fisher's early work on statistical data analysis and experimental design made possible application of scientific method to industrial problems and to the improvement of the quality of everyday life. The use is discussed of simple statistical techniques for informed observation that can be used to improve quality in hospitals and other service organizations as well as in the factory. At a more sophisticated level statistical experimental design may be used by engineers and scientists to design products that rarely go wrong. Experimental design can be employed to maximize a desirable quality characteristic, to minimize its variance, and to make it insensitive to environmental changes. Such expansion of the domain of application of scientific method can not only raise industrial efficiency, but can improve the quality of life for everyone.

Key Words: Sir Ronald Fisher, Scientific Method, Experimental Design, Quality Improvement.

Data Analysis and Experimental Design

Sir Ronald Fisher saw Statistics as the handmaiden of Scientific Investigation. When he first went to Rothamsted in 1919, it was to analyze data on wheat yields and rainfall that extended back over a period of some seventy years. Over the next few years Fisher developed great skill in such analysis, and his remarkable practical sense led in turn to important new theoretical results. In particular, least squares and regression analysis were placed on a much firmer theoretical basis, the importance of graphical methods was emphasized and aspects of the analysis of residuals were discussed.

But these studies presented him with a dilemma. On the one hand such "happenstance" data were affected by innumerable disturbing factors not under his control. On the other hand, if agricultural experiments were run in the laboratory, where complete control was possible, the conclusions might be valueless, since it would be impossible to know to what extent such results applied to crops grown in a farmer's field. The dilemma was resolved by Fisher's invention of statistical experimental design which did much to move science out of the laboratory and into the real world - a major step in human progress.

The theory of experimental design that he developed, employing the tools of blocking, randomization, replication, factorial experimentation and confounding, solved the problem of how to conduct valid experiments in a world which is naturally nonstationary and nonhomogeneous — a world, moreover, in which unseen "lurking variables" are linked in unknown ways with the variables under study, thus inviting misinformation and confusion.

Thus by the beginning of the 1930's Fisher had initiated what is now called statistical data analysis, had developed statistical experimental design and had pointed out their complementary and synergistic nature. Once the value of these ideas was demonstrated for agriculture they quickly permeated such subjects as biology, medicine, forestry and social science.

The 1930's were years of economic depression and it was not long before the potential value of statistical methods to revive and reenergize industry came to be realized. In particular, at the urging of Egon Pearson and others, a new section of the Royal Statistical Society was inaugurated during the next few years, at meetings of the Industrial and Agricultural Section of the Society, workers from academia and industry met to present and discuss applications to cotton spinning, woollen manufacture, glass making, electric light manufacture, and so forth. History has shown that these pioneers were right in their belief that statistical method provided the key to industrial progress. Unhappily their voices were not heard, a world war intervened, and it was at another time and in another country that their beliefs were proved true.

Fisher was an interested participant and frequent discussant at these industrial meetings. He wrote cordially to Shewhart the originator at Bell Laboratories of quality control. He also took note of the role of sampling inspection in rejecting bad products, but he was careful to point out that the rules then in vogue for selecting inspection schemes by setting producer's and consumer's risks, could not, in his opinion, be made the basis for a theory of scientific inference (Fisher 1955). He made this point in a critical discussion of the theory of Neyman and Pearson whose "errors of the first and second kind" closely paralleled producer's and consumer's risks. He could not have forseen that fifty year later the world of quality control would, in the hands of the Japanese, have become the world of quality improvement in which his ideas for scientific advance using statistical techniques of design as well as analysis were employed by industry on the widest possible basis.

The revolutionary shift from quality control to quality improvements which had been initiated in Japan by his long-time friend Dr. W. Edwards Deming, was accompanied by two important concomitant changes; involvement of the whole workforce in quality improvement and recognition that quality improvement must be a continuous and never-ending occupation (see Deming (1986)).

Aspects of Scientific Method

To understand better the logic of these changes it is necessary to consider certain aspects of scientific method. Among living things mankind has the almost unique ability of making discoveries and putting them to use. But until comparatively recently such technical advance was slow - the ships of the thirteenth century wee perhaps somewhat better designed than those of the twelfth century but the differences were not very dramatic. And then three or four hunched years ago a process of quickened technical change began which has ever since been accelerating This acceleration is attributed to an improved process for finding things out which we call scientific method.

We can, I think, explain at least some aspects of this scientific revolution by considering a particular instance of discovery. We are told that in the late seventeenth century it was a monk from the Abbey of Hautvillers who first observed that a second fermentation in wine could be induced which produced a new and different sparkling liquid, delightful to the taste, which we now call champagne. Now the culture of wine itself is known from the earliest records of man and the conditions necessary to induce the production of champagne must have occurred accidentally countless times throughout antiquity. However, it was not until this comparatively recent date that the actual discovery was made. This is less surprising if we consider that to induce an advance of this kind two circumstances must coincide. First an informative event must occur and second a perceptive observer must be present to see it and learn from it.

Now most events that occur in our daily route correspond more or less with what we expect. Only occasionally does something occur which is potentially informative. Also many observers, whether through lack of essential background knowledge or from lack of curiosity or motivation, do not fill the role of a perceptive observer. Thus the slowness in antiquity of the process of discovery can be explained by the extreme rarity of the chance coincidence of two circumstances each of which is itself rare. It is then easily seen that discovery may be accelerated by two processes which I will call informed observation and directed experimentation.

By a process of informed observation we arrange things so that, when a rare potentially informative event does occur people with necessary technical background and motivation are there to observe it. Thus, when last year an explosion of a supernova occurred, the scientific organization of this planet was such that astronomers observed it and learned from it. A quality control chart fills a similar role. When such a chart is properly maintained and displayed it ensures that any abnormality in the routine operation of a process is likely to be observed and associated with what Shewhart called an assignable cause — so leading to the gradual elimination of disturbing factors.

A second way in which the rate of acquisition of knowledge may be increased is by what I will call directed experimentation. This is an attempt to artificially induce the occurrence of an informative event. Thus, Benjamin Franklin's plan to determine the possible connection of lightning and electricity by flying a kite in a thunder cloud and testing the emanations flowing down the string, was an invitation for such an informative event to occur.

Recognition of the enormous power of these methods of scientific advance is now commonplace. The challenge of the modern movement of quality improvement is nothing less than to use them to further, in the widest possible manner, the effectiveness of human activity. By this I mean, not only the process of industrial manufacture, but the running, for example, of hospitals, airlines, universities, bus services and supermarkets. The enormous potential of such an approach had long been forseen by systems engineers (see for example, Jenkins and Youle (1971)) but until the current demonstration by Japan of its practicability, it had been largely ignored.

Organization of Quality Improvement with Simple TooIs

The less sophisticated problems in quality improvement can often be solved by informed observation using some very simple tools that are easily taught to the workforce.

While on the one hand, Murphy's law implacably ensures that anything that can go wrong with a process will eventually go wrong, this same law also ensures that every process produces data which can be used for its own improvement. In this sentence the word process could mean an industrial manufacturing process, or a process for ordering supplies or for paying bills. It could also mean the process of admission to a hospital or of registering at a hotel or of booking an airline flight.

One major difficulty in past methods of system design was the lack of involvement of the people closest to it. For instance, a friend of mine recently told me of the following three incidents that happened on one particular day. In the morning he saw his doctor at the hospital to discuss the results of some test that had been made two weeks before. The results of the tests should have been entered in his records but, as frequently happened at this particular hospital, they were not. The doctor smiled and said rather triumphantly, "Don't worry, I thought they wouldn't be in there. I keep a duplicate record myself although I'm not supposed to. So I can tell you what the results of your tests are." Later that day my friend flew from Chicago to New York and as the plane was taxiing prior to takeoff there was a loud scraping noise at the rear of the plane. Some passengers looked concerned but said nothing. My friend pressed the call button and asked the stewardess about it. She said, "This plane always makes that noise but obviously I can't do anything about it." Finally on reaching his hotel in the evening he found that his room, the reservation for which had been guaranteed, had been given to someone else. He was told that he would be driven to another hotel and that because of the inconvenience his room rate would be reduced. In answer to his protest the reservation clerk said, "I'm very sorry — it's the system. It's nothing to do with me."

In each of these examples the system was itself providing data which could have been used to improve it. But in every case, improvement was frustrated because the physician, the stewardess and the hotel clerk each believed that there was nothing they themselves could do to alter a process that was clearly faulty. Yet each of the people involved was much closer to the system than those who had designed it and who were insulated from receiving data on how it could be improved.

Improvement could have resulted if, in each case, a routine had been in place whereby data coming from the system were automatically used to correct it.

To achieve this it would first have been necessary

to instill the idea that quality improvement was each individual person's responsibility,
to move responsibility for the improvement of the system to a quality improvement team wich included the persons actually involved,
to organize collection of appropriate data (not as a means of apportioning blame, but to provide material for team problem-solving meetings).

The quality team of the hospital records system might include the doctor, the nurse, someone from the hospital laboratory and someone from the records office. For the airplane problem, the team might include the stewardess, the captain, and the person responsible for the mechanical maintenance of the plane. For the hotel problem, the team might include the hotel clerk, the reservations clerk, and someone responsible for computer systems. It is the responsibility of such teams to conduct a relentless and never-ending war against Murphy's regime. Because their studies often reveal the need for additional expertise, and because it will not always be within the power of the team to institute appropriate corrective action, it is necessary that adequate channels for communication exist from the bottom to the top of the organization, as well as from the top to the bottom.

Three potent weapons in the campaign for quality improvement are Corrective Feedback, Preemptive Feedforward and Simplification. The first two are self explanatory. The importance of simplification has been emphasized and well illustrated by F. Timothy Fuller (1986). In the past, systems have tended to become steadily more complicated without necessarily adding any corresponding increase in effectiveness. This occurs when

the system develops by reaction to occasional disasters,
action, supposedly corrective, is instituted by persons remote from the system,
no check is made on whether corrective action is effective or not.

Thus the institution by a department state of complicated safeguards in its system for customer return of unsatisfactory goods might be counter-productive; while not providing sufficient deterence to a mendacious few, it could cause frustration and rejection by a large number of honest customers. By contrast the success of a company such as Marks & Spencer who believe instead in simplification and, in particular, adopt a very enlightened policy toward returned goods, speaks for itself.

Because complication provides work and power for bureaucrats, simplification must be in the hands of people who can benefit from it. The time and money saved from quality improvement programs of this sort far more than compensates for that spent in putting them into effect. No less important is the great boost to the morale of the workforce that comes from their knowing that they can use their creativity to improve efficiency and reduce frustration.

Essential to the institution of quality improvement is the redefinition of the role of the manager. He should not be an officer who conceives, gives and enforces orders but rather a coach who encourages and facilitates the work of his quality teams.

Ishikawa's Seven Tools

At a slightly more sophisticated level the process of informed observation may be facilitated by a suitable set of statistical aids typified, for example, by Ishikawa's seven tools. They are described in an invaluable book available in English (Ishikawa 1976) and written for foremen and workers to study together. The tools are check sheets, Pareto charts, cause-effect diagrams, histograms, graphs, stratification and scatter plots. They can be used for the study of service systems as well as manufacturing systems but I will use an example of the later kind (see, for example, Box and Bisgaard, (1987)).

Suppose a manufacturer of springs finds that at the end of a week that 75 springs have been rejected as defective. These rejects should not be thrown away but studied by a quality team of the people who make them. As necessary, this team would be augmented from time to time with appropriate specialists. A tally on a check sheet could categorize the rejected springs by the nature of the defect. Display of these results on a Pareto chart might then reveal the primary defect to be, say, cracks. To facilitate discussion of what might cause the cracks the members of the quality team would gather around a blackboard and clarify their ideas using a cause-effect diagram. A histogram categorizing cracks by size would provide a clear picture of the magnitude of the cracks and of how much they varied. This histogram might then be stratified, for example, by spring type. A distributional difference would raise the question as to why the cracking process affected the two kinds of springs differently and might supply important clues as to the cause. A scatter plot could expose a possible correlation of crack size with holding temperature and so forth. With simple tools of this kind the team can work as quality detectives gradually "finding and fixing" things that are wrong.

It is sometimes asked if such methods work outside Japan. One of many instances showing that it can, is supplied by a well-known Japanese manufacturer making television sets just outside Chicago in the United States. The plant was originally operated by an American company using traditional methods of manufacture. When the Japanese company first took over the reject rate was 146%. This meant that most of the television sets had to be taken off the line once to be individually repaired and some had to be taken off twice. By using simple "find and fix" tools like those above the reject rate over a period of 4-5 years was reduced from 146% to 2%. Although this was a Japanese company only Americans were employed, and a visitor could readily ascertain that they greatly preferred the new system.

Evolutionary Operation

Evolutionary Operation (EVOP) is an example of how elementary ideas of experimental design can be used by the whole workforce. The central theme (Box 1957 Box and Draper 1969) is that an operating system can be organized which mimics that by which biological systems evolve to optimal forms.

For manufacturing, let us say, a chemical intermediate, the standard procedure is to continually run the process at fixed levels of the process conditions—temperature, flow rate, pressure, and agitation speed and so forth. Such a procedure may be called static operation. However, experience shows that the best conditions for the full scale process are almost always somewhat different from those developed from smaller scale experimentation and furthermore, that some factors important on the full scale cannot always be adequately simulated in smaller scale production. The philosophy of Evolutionary Operation is that the full scale process may be run to produce not only product but also information on how to improve the process and the product. Suppose that temperature and flow rate are the factors chosen for initial study. In the evolutionary operation mode small deliberate changes are made in these two factors in a pattern (an experimental design) about the current best-known conditions. By continuous averaging and comparison of results at the slightly different conditions as they come in, information gradually accumulates which can point to a direction of improvement where for example higher conversion or less impurity can be obtained.

Important aspects of Evolutionary Operation are that

it is an alternative method of continuous process operation. It may therefore be run indefinitely as new ideas evolve and the importance of new factors are realized.
it is run by plant operators as a standard routine with the guidance of the process superintendent and occasional advice from an evolutionary operation committee. It is thus very sparing in the use of technical manpower.
it was designed for improving yields and reducing costs in the chemical and process industries. In the parts industries, where the problem is often that of reducing variation by studying variances instead of means at the various process conditions the process can be made to evolve to one where variation is minimized.

Design of Experiments for Engineers

Informed observation provides ways of doing the best we can on the assumption that the design of the product we produce and the design of the process that produces it are essentially immutable. Obviously a product or process, which suffers from major deficiencies of design, cannot be improved beyond a certain point by these methods. Improvements by Evolutionary Operation are also costrained by what is possible within the basic system. However by artful design it may be possible to arrive at a product and process that have high efficiences and that almost never go wrong. The design of new products and processes is a fertile field for the employment of statistical experimental design.

Which? How? Why?

Suppose y is some quality characteristic whose probability distribution depends on the levels of a number of factors x. Experimental design may be used to reveal certain aspects of this dependence; in particular how the mean E(y) = f(x), and the variance a σ²(y) = F(x), depend on x. Both choice of design and method of analysis are greatly affected by what we know or what we think we know about the input variables x and the Functions f(x) and F(x) (see, for example, Box, Hunter and Hunter (1978)).

Which: In the early stages of investigation the task may be to determine which subset of variables x_k chosen from the larger set x are of importance in affecting y. In this connection a Pareto hypothesis (a hypothesis of "effect sparsity") becomes appropriate and the projective properties into lower dimensions in the factor space of highly fractionated designs (Finney 1945; Plackett and Burman 1946; Rao 1947; Box, Hunter, and Hunter 1978) may be used to find an active subset of k or fewer active factors. Analyses based on normal plots (Daniel 1959) and/or Bayesian methods (Box and Meyer 1986a)) are efficient and geometrically appealing.

How: When we know, or think we know, which are the important variables x_k we may need to determine more precisely how changes in their levels affect y. Often the nature of the functions f(x) and F(x) will be unknown. However over some limited region of interest a local Taylor's series approximation of first or second order in x_k may provide an adequate approximation, particularly if y and x_k are re-expressed, when necessary, in appropriate alternative metrics. Fractional factorials and other response surface designs of first and second order are appropriate here. Maxima may be found and exploited using steepest ascent methods followed by canonical analysis of a fitted second degree equation in appropriately transformed metrics (Box and Wilson 1951). The possibilities for exploiting multidimensional ridges and hence determining alternative optimal process become particularly important at this stage (see, for example, Box and Draper 1986).

Why: Instances occur when a mechanistic model can be postulated. This might take the form of a set of differential equations believed to describe the underlying physics. Various kinds of problems arise. Among these are:

How should parameters (often corresponding to unknown physical constants) be estimated from data?

How should candidate models be tested?

How should we select a model from competing candidates?

What kinds of experimental designs are appropriate?

Workers in quality improvement have so far been chiefly occupied with problems of the "which" and occasionally of the "how" kind and have consequently made most use of fractional factorial designs and other orthogonal arrays, and of response surface designs.

Studying Location, Dispersion and Robustness

In the past experimental design had been used most often as a means of discovering how, for example, the process could be improved by increasing the mean of some quality characteristic. Modern quality improvement also stresses the use of experimental design in reducing dispersion.

Using experimental designs to minimize variation: High quality, particularly in the parts industries (e.g. automobiles, electronics) is frequently associated with minimizing dispersion. In particular, the simultaneous study of the effect of the variables x on the variance as well as the mean is important in the problem of bringing a process on target with smallest possible dispersion (Phadke 1982).

Bartlett and Kendall (1946) pointed to the advantages of analysis in terms of 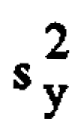to produce constant variance and increased additivity in the dispersion measure. It is also very important in such studies to remove transformable dependence between the mean and standard deviation. Taguchi (1986,1987) attempts to do this by the use of a signal to noise ratios. However, it may be shown that it is much less restrictive, simpler and more statistically efficient to proceed by direct data transformation obtained, for example, by a "lambda plot" (Box 1988).

A practical difficulty may be the very large number of experimental runs which may be needed in such studies if complicated designs are employed. It is recently shown how using what Fisher called hidden replication, unreplicated fractions may sometimes be employed to identify sparse dispersion effects in the presence of sparse location effects (Box and Meyer 1986b)).

Experimental Design and Robustness to the Environment: A well designed car will start over a wide range of conditions of ambient temperature and humidity. The design of the starting mechanism may be said to be "robust" to changes in these environmental variables. Suppose E(y) and possibly also σ²(y) are functions of certain design variables x_d which determine the design of the system and also of sour external environmental variables x_v which, except in the experimental environment, are not under our control. The problem of robust design is to choose a desirable combination of design variables x_do at which good performance is experienced over a wide range of environmental conditions.

Related problems were earlier considered by Youden (1961 a,b) and Wernimont (1975) but recently their importance in quality improvement has been pointed out by Taguchi. His solution employs an experimental design which combines multiplicatively an "inner" design array and an "outer" environmental array. Each piece of this combination is usually a fractional factorial design or some other orthogonal array. Recent research has concentrated on various means for reducing the burdensome experimental effort which presently may be needed for studies of this kind.

Robustness of an assembly to variation in its components: In the design of an assembly, such as an electrical circuit, the exact mathematical relation y = f(x) between the quality characteristic of the assembly, such as the output voltage y of the circuit and the characteristics x of its components (resistors, capacitors, etc.) may be known from physics. However there may be an infinite variety of configurations of x that can give the same desired mean level E(y) = η, say. Thus an opportunity exists for optimal design by choosing a "best" configuration.

Suppose the characteristics x of the components vary about "nominal values" ξ with known covariance matrix V. Thus for example a particular resistance x_i might vary about its nominal value ξ_i with known variance 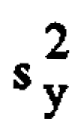. (Also variation in one component would usually be independent of that of another so that V would usually be diagonal). Now variation in the input characteristics x will transmit variation to the quality characteristic y so that for each choice of component nominal values which yield the desired output y = η there will be an associated mean square error = E(y - η)² = M(η) = F(ξ).

Using a Wheatstone Bridge circuit for illustration, Taguchi and Wu (1985) pose the problem of choosing ξ so that M(η) is minimized. To solve it they again employ an experimental strategy using inner and outer arrays. Box and Fung (1986) have pointed out, however, that their procedure does not in general lead te an optimal solution and that it is better to use a simpler and more general method employing a standard numerical nonlinear optimization routine. The latter authors also make the following further points.

For an electrical circuit it is reasonable to assume that the relation y = f(x) is known, but when, as is usually the case, y = f(x) must be estimated experimentally, the problems are much an complicated and require further study.
It is also supposed that each of the 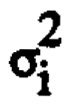are known and furthermore that they remain fixed or change in a known way (for example proportionally) when ξ_i changes. The nature of the optimal solution can be vastly different depending on the validity of such assumptions.

Taguchi's quality engineering ideas are clearly important and present a great opportunity for development It appears, however, (see, for example, Box, Bisgaard and Fung (1988)) that the accompanying statistical methods that Taguchi recommends employing "accumulation analysis," "signal to noise ratios" and "minute analysis" are often defective, inefficient and unnecessarily complicated. Furthermore, Taguchi's philosophy seems at times to imply a substitution of statistics for engineering rather than the use of statistics as a catalyst to engineering (Box 1988). Because such deficiencies can be easily corrected it is particularly unfortunate that, in the United States at least engineers are often taught these ideas by instructors who stress that no deviation from Taguchi's exact recipe is permissible.

A Wider Domain for Scientific Method

Quality improvement is about finding out how to do things better. The efficient way to do this is by using scientific method—a very powerful tool, employed in the past by only a small elite of trained scientists. Modern quality improvement extends the domain of scientific method over a number of dimensions:

over users (e.g. from the chief executive officer to the janitor)
over areas of human endeavor (e.g. factories, hospitals, airlines, department stores)
over time (never-ending quality improvement)
over causative factors (an evolving panorama of factors that affect the operation of a system).
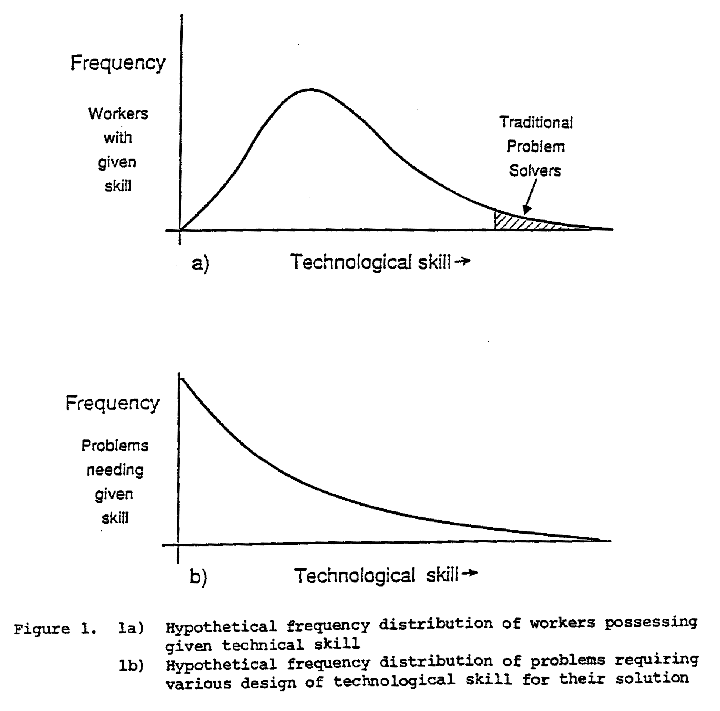
Users: Although it is not possible to be numerically precise I find a rough graphical picture helpful to understanding. The distribution of technological skill in the workforce might look something like Figure 1(a). The distribution of technological skill required to solve the problems, that routinely reduce the efficiency of factories, hospitals, bus companies and so forth, might look something like Figure 1(b).

In the past only those possessing highly trained scientific or managerial talent, would have been regarded as problem solvers. Inevitably this small group could only tackle a small proportion of the problems that beset the organization. One aspect of the new approach is that many problems can be solved by suitably trained persons of lesser technical skills. An organization that does not use this talent throws away a large proportion of its creative potential. A second aspect is that engineers and technologists need to experiment simultaneously with many variables in the presence of noise. Without knowledge of statistical experimental design they are not equipped to do this efficiently.

A group visiting Japanese industry was recently told "an engineer who does not know statistical experimental design is not an engineer? (Box et. al. 1988.)

Areas of Endeavor: At first sight we tend to think of quality improvement as applying only to operations on the factory floor. But even in manufacturing organizations a high proportion of the workforce are otherwise engaged in billing, invoicing, planning, scheduling and so forth all of which should be made the subject of study. But outside such industrial organizations, all of us as individual citizens must deal with a complex world, involving hospitals, government departments, universities, airlines and so forth. Lack of quality in these organizations results in needless expense, wasted time and unnecessary frustration. Quality improvement applied to these activities could free us all for more productive and pleasurable pursuits.

Time: For never-ending improvement there must be a long-term commitment to renewal. A commonly used statistical model links a set of variables x_k with a response y by an equation y = f(x_k) + e where e is an error term, often imbued by statisticians with properties of randomness, independence and normality. A more realistic version of this model is

y = f(x_k) + e(x_u)

where x_u is a set of variables whose nature and behavior is unknown. By skillful use of the techniques of informed observation and experimental design, as time elapses, elements of x are transferred into x_k — from the unknown into the known. This transference is the essence of modem quality improvement and has two consequences:

once a previously unknown variable has been identified it can be fixed at a level that produces the best results.
by fixing it we remove an element previously contributing to variation.

This transfer can be a never-ending process whereby knowledge increases and variation is reduced.

The structure of the process of investigation so far as it involves statistics has not always been understood. It has sometimes been supposed that it consists of testing a null hypothesis selected in advance against an alternative using a single set of data. In fact most investigations proceed in an iterative fashion in which deduction and inductionproceed in alternation (see, for example, Box (1980)). Clearly optimization of individual steps in such a process can lead to sub-optimization for the investigational process itself. The inferential process of estimation whereby a postulated model and supposedly relevant data are combined is purely deductive. It is conditional on the assumption that the model of the data generating process and the actual process itself are consonant No warning that they are not consonant is provided by estimation. However a comparison of appropriate qualities derived from the data with a sampling reference distribution generated by the model provides a process of criticism that can not only discredit the model but suggest an appropriate direction for model modification. An elementary example of this is Shewhart's idea of an "assignable cause" deduced from data falling outside control lines which are calculated from a model of the data-generating process in a state of control. Such a process of criticism contrasts features of the model and the data. It can lead the engineer, scientist or technologist by a process of induction to postulate a modified, or a totally different model, so recharting the course for further exploration. This process is subjective and artistic. It is the only step that can introduce new ideas and hence must be encouraged above all else. It is best encouraged, I believe, by interactive graphical analysis and is readily provided these days by computers. Such devices also make it possible to use sophisticated statistical ideas that are calculation-intensive and yet produce simply understood graphical output. It is by following such a deductive-inductive iteration that the quality investigator can be led to a solution of a problem just as a good detective can solve a mystery.

Factors and Assignable Causes: The field of factors potentially important to quality improvement also can undergo seemingly endless expansion. Problems of optimization are frequently posed as if they consisted of maximizing some response y over a k-dimensional space of known factors x_k, but in quality improvement the factor space is never totally known and is continually developing.

Consider a possible scenario for a problem which begins as that of choosing the reaction time x₁ and reaction temperature x₂ to give maximum conversion y of raw materials to the desired product. Suppose experimentation with these two factors leads to the (conditional) optimal choice of coordinates in Figure 2(a). Since conversion is only 56% we see that the best is not very good if we restrict experimentation to these two variables. After sonic deliberation it is now suggested that higher conversion might be obtained if by-products which may be being formed at the beginning of the reaction are suppressed by employing a lower temperature in the early stages. This idea produces two new variables, the initial temperature x₃ and the time x₄ taken to reach the final temperature. Their best values, and the appropriately changed levels of x₁ and x₂, might be those shown in Figure 2(b). This new (conditional) optimal profile again results in only partial success (y = 68%) leading to the suggestion that the (newly increased) final temperature may result in other biproducts being formed at the later stages of reaction. This suggests experimentation with variables x₅ and x₆ allowing for a fall off in temperature towards the end of the reaction. The new (conditional) optimal profile arrived at by experimentation with six variables might then be as in Figure 2(c).

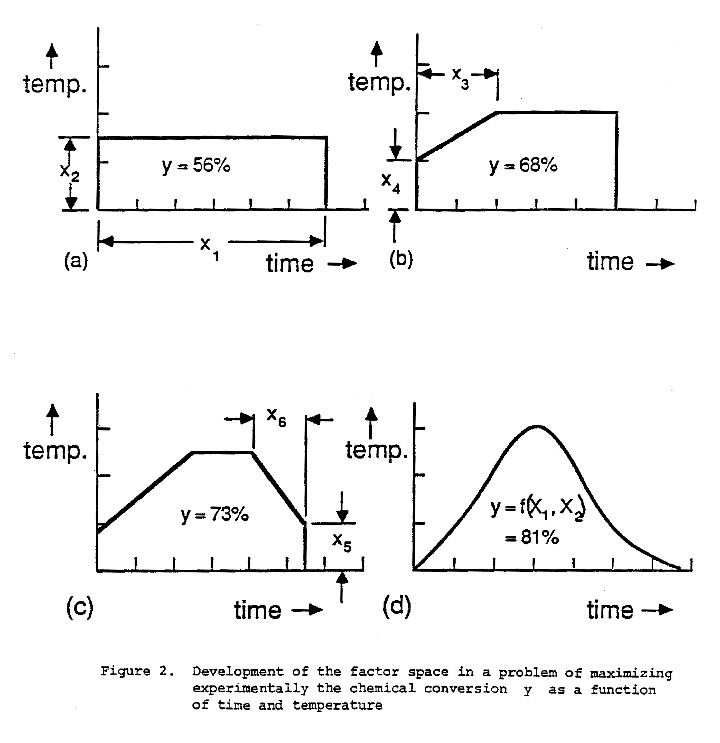
These results might now be seen by a physical chemist leading him to suggest a mechanistic theory yielding a series of curved profiles which depended on only two (unknown) theoretical quantities X₁ and X₂. If this idea was successful the introduction of these two new quantities as experimental factors would have eliminated the need for the other six. This new mechanistic theory might then in turn suggest new factors, not previously thought of, which might produce even greater conversion, and so on. Thus the factor space must realistically be regarded as one which is continually changing and developing. This can be thought of as part of the evolution which occurs within the scientific process in a manner discussed earlier by Kuhn (1962).

Training

Instituting the necessary training for quality is a huge and complex task. Some assessment must be made of the training needs for the workforce, for engineers, technologists and scientists, and for managers at various levels, and we must consider how such training programs can be organized using the structure that we have within industry, service organizations, technical colleges and universities. A maximum multiplication effect will be achieved by a scheme in which the scarce talent that is available is employed to teach the teachers within industry and elsewhere. It is, I believe, unfortunately true that the number of graduates who are interested in industrial statistics in Great Britain has been steadily decreasing. The masons for this are complex and careful analysis and discussion between industry, the government, and the statistical fraternity is necessary to discover what might be done to rectify the situation.

Management

The case for the extension of scientific method to human activities is so strong and so potentially beneficial that one may wonder why this revolution has not already come about. A major difficulty is to persuade the managers.

In the United States it is frequently true that both higher management and the workforce are in favor of these ideas. Chief executive officers whose companies are threatened with extinction by foreign competition are readily convinced and are prepared to exhort their employees to engage in quality improvement. This is certainly a step in the right direction but it is not enough. I recently saw a poster issued jointly by the Union and the Management of a large automobile company in the United States which reiterated a Chinese proverb "Tell me —I'll forget; Show me— I may remember; Involve me and I'll understand". I'm not sure that top management always realize that their involvement (not just their encouragement) is essential. The workforce enjoy taking part in quality improvement and will cooperate provided they believe that the improvements they bring about will not be used against them.

Some members of the middle levels of management and of the bureaucracy pose a more serious problem because they see loss of power in sharing the organization of quality improvement with others. Clearly the problems of which W. Gorbachev complains in applying his principles of perestroika are not confined the Soviet Union.

Thus the most important questions are really not concerned so much with details of the techniques but with whether process of change in management can be brought about so that they can be used at all. It is for this reason that Dr. Deming and his followers have struggled so hard with this most difficult problem of aIl — that of inducing the changes in management and instituting the necessary training that can allow the powerful tools of scientific method to be used for quality improvement. It is ton the outcome of this struggle that our economic future ultimately depends.

Fisher's Legacy

At the beginning of this lecture I portrayed Fisher as a man who developed statistical methods of design and analysis that extended the domain of science from the laboratory to the whole world of human endeavor. We have the opportunity now to bring that process to full fruition. If we can do this we can not only look forward to a rosier economic future, but by making our institutions easier to deal with, we can improve the quality of our everyday lives, and most important of all we can joyfully experience the creativity which is a part of every one of us.

Acknowledgement

This research was sponsored by the National Science Foundation under Grant No. DMS-8420968, the United States Army under Contract NO. DAALO3-87K-0050, and by the Vilas Trust of the University of Wisconsin-Madison.

References

Bartlett, M.S. and D.G. Kendall (1946) The statistical analysis of variance -heterogeneity and the logarithmic transformation. J. Roy. Statist. Soc., Ser B 8, 128-150.
Box, G.E.P. (1957) Evolutionary Operation: A method for increasing industrial productivity. Applied Statistics 6, 3-23.
Box, G.E.P. (1980) Sampling and Bayes inference in scientific modelling and robustness. J. Roy. Statist.Soc., Ser A, 143, 383-404.
Box, G.E.P. (1988) Signal-to-noise ratios, performance criteria and transformations. Technometrics 30, 1-17.
Box, G.E.P. and S. Bisgaard (1987) The scientific context of quality improvement. Quality Progress, 20, No.6, 54-61.
Box, G.E P., Bisgaard S., and CA. Fung (1988) An explanation and critique of Taguchi's contributions to quality engineering. Report No. 28, Center for Quality and Productivity Improvement, University of Wisconsin-Madison. To appear: Quality and Reliabillry Engineering International, May 1988.
Box, G.E.P. and N.R. Draper (1969) Evolutionary Operation-A statistical method for process improvement New York: Wiley.
Box, G.E.P. and N.R. Draper (1986) Empirical model-building and response surfaces, New York: Wiley.
Box, G.E.P. and C. A. Fung (1986) Studies in quality improvement: Minimizing transmitted variation by parameter design. Report No.8, Center for Quality and Productivity Improvement, University of Wisconsin Madison.
Box, G.E.P., Hunter, W.G., and J.S. Hunter (1978) Statistics for Experimenters: An introduction to design, data analysis, and model building. New York: Wiley.
Box, G.E.P., Kackar, R.N., Nair, V.N., Phadke, M., Shoemaker, A.C., and C.F. J. Wu (1988) Quality Practices in Japan. Quality Progress, XX, No.3, pp 37-41.
Box, G.E.P and R.D. Meyer (1986a) An analysis for unreplicated fractional factorials.Technometrics 28, 11-18.
Box, G.E.P. and RD. Meya (1986b) Dispersion effects from fractional designs. Technometrics 28, 19-27.
Box, G.E.P. and K.B. Wilson (1951) On the experimental attainment of optimum conditions. J. Roy. Statist. Soc., Ser B 8, 1-45.
Daniel, C. (1959) Use of half-normal plots in interpreting factorial two-level experiments. Technometrics, 1, 311-341.
Deming, W.E. (1986) [a href= "http://management.curiouscat.net/books/175-Out-of-the-Crisis"] Out of the crisis[/a], Cambridge MA, MIT Press.
Finney, D.J. (1945) The factorial replication of factorial arrangements. Annals of Eugenics, 12, 291-301.
Fisher, R.A. (1955) Statistical methods and scientific induction. J. Roy. Statist. Soc., Ser. B, 17, 69-78
Fuller, F.T. (1986) Eliminating complexity from work: improving productivity by enhancing quality. Report No. 17, Center for Quality and Productivity Improvement, University of Wisconsin-Madison.
Ishikawa, K. (1976) Guide to quality control, Asian Productivity Organization.
Jenkins, G.M. and P.V. Youle (1971) Systems engineering. London; G.A. Watts.
Kuhn, T. (1962) The Structure of Scientific Revolutions. University of Chicago Press, Chicago.
Phadke, M.S. (1982) Quality engineering using design of experiments. Proceedings of the section on Statistical Education, American Statistical Association, 11-20.
Plackett, R.L. and J.P. Burman (1946) Design of optimal multifactorial experiments. Biometrika, 23, 305-325.
Rao, C.R. (1947) Factorial experiments derivable from combinatorial arrangements of arrays. J. Roy. Statist. Soc., Ser B 9, 128-140.
Taguchi, G. (1986) Introduction to quality engineering: Designing quality into products and processes. White Plains, N.Y.: Kraw International Publications.
Taguchi, G. (1987) System of experimental design. Vol 1 and 2, White Plains, NY: Kraus International Publications.
Taguchi, G. and Y. Wu (1985) Introduction to off-line quality control. Nagaya Japan: Central Japan Quality Control Association.
Wernimont, G. (1977) Ruggedness evaluation of test procedures. Standardization News, 5, 13-16.
Youden, W.J. (1961a) Experimental design and ASTM committees. Materials research and standards, 1,862-867, Reprinted in Precision Measurement and Calibration, Special Publication 300, National Bureau of Standards, Vol. 1, 1969, Editor H. R Ku.
Youden, W.J. (1961b) Physical measurement and experimental design. Collogues Internationaux du Centre National de la Recheiche Scientifique No 110, le Plan d'Experiences, 1961, 115-128. Reprinted in Precision Measurement and Calibration, Special Publication 300, National Bureau of Standards, Vol.1,1969, Editor H. H. Ku.